TEKNIK ANALISIS DATA PENELITIAN KUANTITATIF (ANALISIS KUANTITATIF)

 

Teknik Analisis Data dalam Penelitian Kuantitatif (Analisis Kuantitatif). Analisis kuantitatif dalam suatu penelitian dapat didekati dari dua sudut pendekatan, yaitu analisis kuantitatif secara deskriptif, dan analisis kuantitatif secara inferensial. Masing-masing pendekatan ini melibatkan pemakaian dua jenis statistik yang berbeda. Yang pertama menggunakan statistik deskriptif dan yang kedua menggunakan stastistik inferensial. Kedua jenis statistik ini memiliki karakteristik yang berbeda, baik dalam hal teknik analisis maupun tujuan yang akan dihasilkannya dari analisisnya Sesuai dengan namanya, deskriptif hanya akan mendeskripsikan keadaan suatu gejala yang telah direkam melalui alat ukur kemudian diolah sesuai dengan fungsinya. Hasil pengolahan tersebut selanjutnya dipaparkan dalam bentuk angka-angka sehingga memberikan suatu kesan lebih mudah ditangkap maknanya oleh siapapun yang membutuhkan informasi tentang keberadaan gejala tersebut. Dengan demikian hasil olahan data dengan statistik ini hanya sampai pada tahap deskripsi, belum sampai pada tahap generalisasi. Dengan kata lain, statistik deskriptif adalah statistik yang mempunyai tugas mengorganisasi dan menganalisa data angka, agar dapat memberikan gambaran secara teratur, ringkas dan jelas, mengenai suatu gejala, peristiwa atau keadaan, sehingga dapat ditarik pengertian atau makna tertentu.

 

Statistik inferensial fungsinya lebih luas lagi, sebab dilihat dari analisisnya, hasil yang diperoleh tidak sekedar menggambarkan keadaan atau fenomena yang dijadikan obyek penelitian, melainkan dapat pula digeneralisasikan secara lebih luas kedalam wilayah populasi. Karena itu, penggunaan statistik inferensial menuntut persyaratan yang ketat dalam masalah sampling, sebab dari persyaratan yang ketat itulah bisa diperoleh sampel yang representatif; sampel yang memiliki ciri-ciri sebagaimana dimiliki populasinya. Dengan sampel yang representatif maka hasil analisis inferensial dapat digeneralisasikan ke dalam wilayah populasi.

 

 

1. Jenis Data dalam Penelitian Kuantitatif

Sudah dikenal bahwa statistik merupakan salah satu cara yang banyak manfaatnya bagi peneliti untuk menganilis data. Satu modal penting yang harus dikuasai terlebih dahulu oleh peneliti yang akan menggunakan teknik statistik adalah pengertian mengenai jenis data yang akan dianalisis, agar penggunaan data kuantitatif untuk keperluan analisis statistik tepat sasaran. Atau sebaliknya, pemilihan jenis teknik statistik dapat dipilih secara tepat sesuai dengan sifat-sifat atau jenis-jenis data yang dihadapi.

 

Dalam dunia statistik dikenal setidaknya terdapat empat jenis data hasil pengukuran, yaitu data Nominal, Ordinal, Interval dan Rasio. Masing-masing data hasil pengukuran  ini memiliki karaktristik tersendiri yang berbeda antara satu dengan lainnya.

 

1. Data Nominal

Data ini juga sering disebut data diskrit, kategorik, atau dikhotomi. Disebut diskrit karena ini data ini memiliki sifat terpisah antara satu sama lainnya, baik pemisahan itu terdiri dari dua bagian atau lebih; dan di dalam pemisahan itu tidak terdapat hubungan sama sekali. Masing-masing kategori memiliki sifat tersendiri yang tidak ada hubungannya dengan kategori lainnya. Sebagai misal data hasil penelitian dikategorikan kedalam kelompok “ya” dan “tidak” saja misalnya  laki-laki/wanita (laki-laki adalah ya laki-laki; dan wanita adalah “tidak laki-laki”), kawin /tidak kawin; janda/duda, dan lainnya.

 

Data nominal selain contoh di atas terdapat pula yang berupa angka-angka. Akan tetapi angka-angka tersebut bukan merupakan suatu atribut, oleh sebab itu pada angka tersebut tidak berlaku hitungan matematis. Contoh data ini misalnya nomor punggung pemain sepak bola, nomor rumah, nomor plat mobil dan lainnya. Nomor-nomor tersebut semata-semata hanya menunjukkan simbol, tanda, atau stribut saja.

 

2. Data Ordinal

Data ordinal adalah data yang menunjuk pada tingkatan atau penjenjangan pada sesuatu keadaan. Berbeda  dengan data nominal yang menunjukkan adanya perbedaan secara kategorik, data ordinal juga memiliki sifat adanya perbedaan di antara obyek yang dijenjangkan. Namun dalam perbedaan tersebut terdapat suatu kedudukan yang dinyatakan sebagai suatu urutan bahwa yang satu lebih besar atau lebih tinggi daripada yang lainnya.Kriteria urutan dari yang paling tinggi ke yang yang paling rendah dinyatakan dalam bentuk posisi relatif atau kedudukan suatu kelompok. Contoh dari data ini misalnya: prestasi belajar siswa diklasifikasikan menjadi kelompok “baik”, “cukup”, dan “kurang”, atau ukuran tinggi seseorang  dengan “tinggi”, “sedang”, dan “pendek”.

 

Dalam kaitannya dengan analisis data, terhadap data ordinal seringkali diberikan “skor’ sesuai dengan tingkatannya. Istilah “skor” diberi tanda petik karena skor tersebut bukan skor sebenarnya, tetapi sebagai “tanda” yang menunjukkan tingkatan.

Dalam kaitannya dengan analisis data, terhadap data ordinal seringkali diberikan “skor’ sesuai dengan tingkatannya. Istilah “skor” diberi tanda petik karena skor tersebut bukan skor sebenarnya, tetapi sebagai “tanda” yang menunjukkan tingkatan.

Contoh:           “Baik”             ……..  diberi tanda 3

“Cukup”          ……..  diberi tanda 2

 “Kurang”        ……..  diberi tanda 1

 

Contoh lain data ordinal misalnya hasil ujian mahasiswa peserta kuliah Statistik Pendidikan Budiman memperoleh skor 90, Rahmat 85, Musyafak 75, dan Mahsunah 65. Berdasarkan skor-skor tersebut dibuatlah suatu jenjang  (rangking), sehingga terjadilah urutan jenjang ke 1 (90), ke 2 (85), ke 3 (75), dan ke 4 (65).Data ordinal memiliki harga mutlak (dapat diperbandingkan) dan selisih perbedaan antara urut-urutan yang berdekatan bisa tidak sama. Data ordinal mempunyai nilai yang lebih tinggi dibandingkan dengan data diskrit karena mempunyai tingkatan yang lebih banyak daripada data diskrit yang hanya mempunyai dua kategori yaitu “ya” dan “tidak”

 

3. Data Interval

Data interval tergolong data kontinum yang mempunyai tingkatan yang lebih tinggi lagi dibandingkan dengan data ordinal karena mempunyai tingkatan yang lebih banyak lagi. Data interval menunjukkan adanya jarak antara data yang satu dengan yang lainnya. Contoh data interval misalnya indeks prestasi mahasiswa dan hasil tes psikologi. Satu hal yang perlu diperhatikan bahwa data interval tidak dikenal adanya nilai 0 (nol) mutlak. Dalam hasil pengukuran (tes) misalnya mahasiswa mendapat nilai 0. Angka nol ini tidak dapat diartikan bahwa mahasiswa tersebut benar-benar tidak bisa apa-apa. Meskipun ia memperoleh nilai nol ia memiliki suatu pengetahuan atau kemampuan dalam matakuliah yang bersangkutan. Nilai nol yang diberikan oleh dosen sebetulnya hanya merupakan atribut belaka hanya saja pada saat ujian, pertanyaan yang diujikan tidak pas seperti yang dipersiapkannya. Atau jawaban yang diberikan tidak sesuai dengan yang dikehendaki soal.

 

4. Data Rasio

Data rasio merupakan data yang tergolong ke dalam data kontinum juga tetapi yang mempunyai ciri atau sifat tertentu. Data ini memiliki sifat interval atau jarak yang sama seperti halnya dalam skala interval. Namun demikian, skala rasio masih memiliki ciri lain. Pertama harga rasio memiliki harga nol mutlak,  artinya titik nol benar-benar menunjukkan tidak adanya suatu ciri atau sifat. Misalnya titik nol pada skala sentimeter menunjukkan tidakadanya panjang atau tinggi sesuatu. Kedua angka skala rasio memiliki kualitas bilangan riel yang berlaku perhitungan matematis. Misalnya berat badan Rudi  70 kg, sedangkan Saifullah 35 kg. Keadaan ini dapat dirasiokan bahwa berat badan Rudi dua kali berat badan Saifullah. Atau berat badan Saifullah separuh dari berat badan Rudi. Berbeda dengan data interval misalnya Rudi  ujian dapat 70 sementara Saifullah memperoleh 30. Hal ini tidak dapat diartikan  bahwa kepandaian Rudi  dua kali lipat kepandaian Saifullah.

 

2. Statistik Deskriptif dan Inferensial

Statistik deskriptif adalah statistik yang digunakan untuk menganalisis data dengan cara mendeskripsikan atau menggambarkan data yang telah terkumpul sebagaimana adanya tanpa bermaksud membuat kesimpulan yang berlaku untuk umum atau generalisasi. Penelitian yang dilakukan pada populasi (tanpa diambil sampel) jelas akan menggunakan statistik deskriptif dalam analisisnya. Tetapi bila penelitian dilakukan pada sampel, maka analisisnya dapat menggunakan statistik deskriptif dan inferensial statistik deskriptif dapat digunakan bila peneliti hanya ingin mendeskripsikan data sampel dan tidak ingin membuat kesimpulan yang berlaku untuk populasi di mana sampel diambil. Tetapi bila peneliti ingin membuat kesimpulan yang berlaku untuk populasi, maka teknik analisis yang digunakan adalah statistik inferensial.

 

Termassuk dalam statistik deskriptif antara lain penyajian data melalui tabel, grafik, diagram lingkaran, penghitungan modus, median, mean, penghitungan desil, persentil, penghitungan penyebaran data melalui perhitungan rata-rata dan standar deviasi, perhitungan persentasi. Dalam statistik deskriptif juga dapat dilakukan mencari kuatnya hubungan variabel melalui analisis korelasi, melakukan prediksi dengan analisis regresi, dan membuat perbandingan dengan membandingkan rata-rata data sampel atau populasi. Hanya perlu diketahui bahwa dalam analisis korelasi, regresi, atau membandingkan dua rata-rata atau lebih tidak perlu diuji signifikansinya. Jadi secara teknis dapat diketahui dalam statistik deskriptif tidak ada uji signifikansi, tidak ada taraf kesalahan, karena peneliti tidak bermaksud membuat generalisasi sehingga tidak ada kesalahan generalisasi.

 

Statistik inferensial (sering juga disebut statistik induktif) adalah teknik statistik yang digunakan untuk menganalisis data sampel dan hasilnya diberlakukan untuk populasi. Statistik ini akan cocok digunakan bila sampel diambil dari populasi yang jelas dan teknik pengambilan sampel dari populasi itu dilakukan secara random.

 

Statistik ini disebut dengan statistik probabilitass karena kesimpulan yang diberlakukan untuk populasi berdasarkan data sampel itu kebenarannya bersifat peluang. Suatu kesimpulan dari data sampel yang akan diberlakukan untuk populasi itu memmpunyai peluang kesalahan dan kebenaran yang dinyatakan dalam bentuk persentase. Bila peluang kesalahan 5% maka taraf kepercayaan 95%, bila peluang kesalahan 1%, maka taraf kepercayaan 99%. Peluang kesalahan dan kepercayaan ini disebut dengan taraf signifikansi. Jadi signifikansi adalah kemampuan untuk digeneralisasikan dengan kesalahan tertentu. Ada hubungan signifikan berarti hubungan itu dapat digeneralisasikan. Ada perbedaan berarti perbedaan itu dapat digeneralisasikan.

 

3. Statistik Parametris dan Nonparametris

Statistika inferensial meliputi statistik parametris dan nonparametris. Statistik parametris digunakan untuk menguji parameter populasi melalui statistik, atau menguji ukuran populasi melalui data sampel. Penggunaan statistik parametris dan nonparametris bergantung pada asumsi dan jenis data yang akan dianalisis. Statistik parametris memerlukan terpenuhi banyak asumsi. Asumsi yang utama adalah data yang akan dianalisis harus berdistribusi normal. Selanjutnya dalam penggunaan salah satu test mengharuskan data dua kelompok atau lebih yang diuji harus homogen, dalam regresi harus terpenuhi asumsi linieritas. Statistik nonparametris tidak menuntut terpenuhi banyak asumsi, misalnya data yang akan dianalisis tidak harus berdistribusi normal. Oleh karena itu, statistik nonparametris sering disebut bebas distribusi.

 

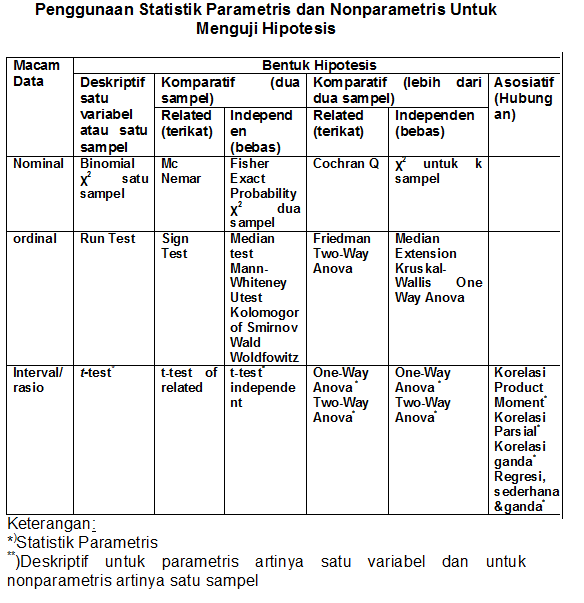
Penggunaan kedua statistik tersebut juga bergantung pada jenis data yang dianalisis. Statistik parametris kebanyakan digunakan untuk menganalisis data interval dan data rasio, sedangkan nonparametris kebanyakan digunakan untuk menganalisis data nominal dan ordinal. Pada tabel berikut ditunjukkan penggunaan statistik parametris dan nonparametris untuk analisis data khususnya untuk pengujuan hipotesis. Di dalam tabel terlihat bahwa statistik parametris digunakan untuk menganalisis data interval dan rasio, dan nonparametris digunakan untuk data nominal dan ordinal. Jadi untuk menguji hipotesis dalam penelitian kuantitatif yang menggunakan statistik ada dua hal utama yang diperhatikan yaitu jenis data dan hipotesis yang diajukan.

Berdasarkan tabel di atas dapat dikemukakan di sini bahwa:

1.     Untuk menguji hipotesis deskriptif satu sampel bila datanya nominal, maka digunakan teknik statistik

•            Binomial

•            Chi kuadrat satu sampel

2.     Untuk menguji hipotesis deskripstif satu sampel bila datanya berbentuk ordinal maka digunakan teknik statistik

•            Run test

3.     Untuk menguji hipotesis deskriptif satu variabel bila datanya berbentuk interval atau ratio maka digunakan t-test satu sampel.

4.     Untuk menguji hipotesis komparatif dua sampel yang berpasangan bila datanya berbentuk nominal digunakan teknik statistik.

•            Mc Nemar

5.     Untuk menguji hipotesis komparatif dua sampel yang berpasangan bila datanya berbentuk ordinal digunakan teknik statistik.

•            Sign test

•            Wilcoxon matced pairs

6.     Untuk menguji hipotesis komparatif dua sampel yang berpasangan bila datanya berbentuk intercal atau ratio digunakan teknik statistik.

7.     Untuk menguji hipotesis komparatif dua sampel independen bila datanya berbentuk nominal digunakan teknik statistik.

•            Fisher exact probability

•            Chi kuadrat dua sampel

8.     Untuk menguji hipotesis komparatif dua sampel independen bila datanya berbentuk ordinal digunakan teknik statistik

•            Median test

•            Mann-Whitney U test

•            Kolmogorov Smirnov

•            Wald-Wolfowitz

9.     Untuk menguji hipotesis komparatif dua sampel yang berpasangan bila datanya berbentuk interval atau ratio digunakan teknik statistik.

10. Untuk menguji hipotesis komparatif k sampel berpasangan, bila datanya berbentuk nominal digunakan teknik statistik

•            Chocran Q

11. Untuk menguji hipotesis komparatif k sampel berpasangan, bila datanya berbentuk ordinal digunakan teknik statistik

•            Friedman Two-way Anova

12. Untuk menguji hipotesis komparatif sampel berpasangan, bila datanya berbentuk interval atau rasio  digunakan analisis varians satu jalan maupun dua jalan.

13. Untuk menguji hipotesis komparatif k sampel independen, bila datanya berbentuk nominal digunakan teknik statistik

•            Chi kuadrat k sampel

14. Untuk menguji hipotesis komparatif k sampel independen, bila datanya berbentuk ordinal digunakan teknik statistik

•            Median extension

•            Kruskal-Wallis One-Way Anova

15. Untuk menguji hipotesis asosiatif bila datanya berbentuk nominal digunakan teknik statistik

•            Koefisien Kontingensi

16. Untuk menguji hipotesis asosiatif bila datanya berbentuk ordinal digunakan teknik statistik.

•            Korelasi Spearman Rank

•            Korelasi Kendal Tau

17. Untuk menguji hipotesis asosiatif bila datanya berbentuk interval atau ratio digunakan.

•            Korelasi Produk Moment: untuk menguji hipotesis hubungan antara satu variabel independen dan variabel dependen.

•            Korelasi ganda bila untuk menguji hipotesis tentang hubungan dua variabel independen atau lebih secara bersama-sama dengan variabel dependen.

•            Korelasi Parsial digunakan untuk menguji hipotesis hubungan antara dua variabel atau lebih bila terdapat variabel yang dikendalikan

•            Analisis regresi digunakan untuk melakukan prediksi, bagaimana perubahan nilai variabel independen dinaikkan atau diturunkan nilainya.

Demikian materi pembelajaran Metodelogi Penelitian tentang Teknik Analisis Data dalam Penelitian Kuantitatif (Analisis Kuantitatif), semoga ada manfaatnya.

= Baca Juga =